GMAT Algebra in Detail
To tackle GMAT effectively, a root level knowledge of the syllabus is of utmost importance. This knowledge not only helps in defining the boundaries of the test but also for assessing one’s strengths and weaknesses in the areas.
Let’s look at the GMAT-Quant: Algebra syllabus in detail. The questions from Algebra part can be from the following topics:
1. Absolute Values: Absolute value is the magnitude of a real number without regard to its sign. E.g. |-2| = 2 and |2| = 2. Here irrespective of the sign the value is always 2. The symbol || is called the modulus.
2. Exponential Equations: In exponential equations, the variable is located in the exponent or power. E.g. ax = ay then x=y (when a is a non zero entity.) In this equation a is called the base, x, and y are called the exponents. The whole equation is called an exponential equation.
Basic laws
of exponents are:
3.
Exponential
Powers: Exponential powers
define the number of times the base has to be multiplied by itself.
E.g. 23 = 2*2*2. That is the base 2 is to be multiplied
3 times which is the exponent. The basic laws of exponential powers are:
4.
Roots
and Radicals: Radical is the opposite
to the exponent power operation.
E.g.
Consider,√2. The square root is called Radical
and the number 2 is called Radicant. To define a cube root, a 3
is placed on the radical and for a fourth root a 4 and so on. Some common operations include:
Memorizing
these squares and radicals will help in beating the time at the exam.
5. Inequalities: Inequalities basically defines how different two quantities are.
The less than (<), greater than (>), less than or equal (<=), greater than or equal (>=) and not equal to (≠) operators are the general symbols used for comparison between equations and numerical values.
6. Linear Equations: Linear equations are the equations in which the maximum powers of a variable is 1.
E.g. X+Y+2=0 is a linear equation because the highest power of X/Y in the equation is ‘1’. As opposed to non-linear equations whose powers are not 1. E.g. X-2 +Y-2 + 2 = 0.
7. Order of Operations: When proceeding to deal with a complex set of operations, there is a need to consider the order by which the mathematical problem should be approached.
E.g. Consider the equation, (3+4*6+(5+4)), this can have results like 51 if we proceed from left to right, or 55 if we proceed from the right to left. But both the results are wrong and the correct answer is 36.
A simple rule is to memorize the order of operations. P – Parentheses E – Exponents M – Multiplication D – Division A – Addition S – Subtraction.
8.
Quadratic
Equations: If the maximum
powers of variables, in an equation, is ‘2’ then that equation is
considered as a Quadratic Equation.
E.g. X2
+2XY +Y2 = 0 is said to
be a quadratic equation. Memorizing the factoring methods and the quadratic
root formula can help in winning time in the test.
·
a2–b2=(a+b)(a−b).
·
a2+2ab+b2=(a+b)2.
·
a2–2ab+b2=(a−b)2
.
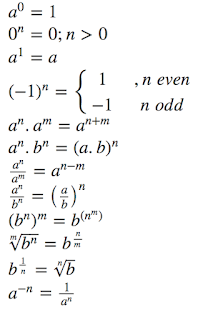



Comments
Post a Comment